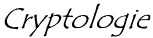|
|
Le 15 mai 1973 le NBS (National Bureau of Standards, aujourd'hui appelé NIST - National Institute of Standards and Technology) a lancé un appel dans le Federal Register (l'équivalent aux Etats-Unix du Journal Officiel en France) pour la création d'un algorithme de chiffrement répondant aux critères suivants:
C'est un système de chiffrement par blocs de 64 bits, dont 8 bits (un octet) servent de test de parité (pour vérifier l'intégrité de la clé). Chaque bit de parité de la clef (1 tous les 8 bits) sert à tester un des octets de la clef par parité impaire, c'est-à-dire que chacun des bits de parité est ajusté de facon à avoir un nombre impair de '1' dans l'octet à qui il appartient. La clé a donc une longueur "utile" de 56 bits, ce qui signifie que seuls 56 bits servent dans l'algorithme. L'algorithme consiste à faire des combinaisons, des substitutions et des permutations entre le texte à chiffrer et la clé, en faisant en sorte que les opérations puissent se faire dans les deux sens (pour le déchiffrement). On appelle code produit la combinaison entre substitutions et permutations. La clé est codée sur 64 bits et formée de 16 blocs de 4 bits, généralement notés k1 à k16. Etant donné que "seulement" 56 bits servent réellement à chiffrer, il y a 256 (soit 7.2*1016) possibilités de clés différentes !
Les grandes lignes de l'algorithme sont les suivantes:
Dans un premier temps, chaque bit d'un bloc est soumis à la permutation initiale, pouvant être représentée par la matrice de permutation initiale (notée PI) suivante :
Cette matrice de permutation indique, en parcourant la matrice de gauche à droite puis de haut en bas, que le 58ème bit du bloc de texte de 64 bits se retrouve en première position, le 50ème en seconde position et ainsi de suite.
Une fois la permutation initiale réalisée, le bloc de 64 bits est scindé en deux blocs de 32 bits, notés respectivement G et D (pour gauche et droite, la notation anglo-saxonne étant L et R pour Left and Right). On note G0 et D0 l'état initial de ces deux blocs :
Il est intéressant de remarquer que G0 contient tous les bits possédant une position paire dans le message initial, tandis que D0 contient les bits de position impaire.
Les blocs Gn et Dn sont soumis à un ensemble de transformation itératives appelées rondes, explicitées dans ce schéma, et dont les détails sont donnés plus bas :
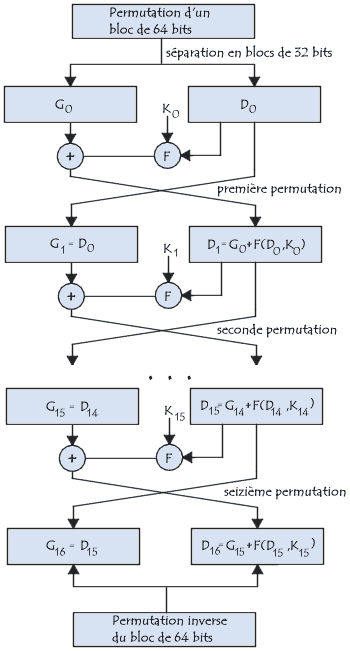
Les 32 bits du bloc D0 sont étendus à 48 bits grâce à une table (matrice) appelé table d'expansion (notée E), dans laquelle les 48 bits sont mélangés et 16 d'entre eux sont dupliqués :
Ainsi, le dernier bit de D0 (c'est-à-dire le 7ème
bit du bloc d'origine) devient le premier, le premier devient le second, ...
La matrice résultante de 48 bits est appelée D'0 ou bien E[D0]. L'algorithme DES procède ensuite à un OU exclusif entre la première clé K1 et E[D0]. Le résultat de ce OU exclusif est une matrice de 48 bits que nous appelerons D0 par commodité (il ne s'agit pas du D0 de départ!).
D0 est ensuite scindé en 8 blocs de 6 bits, noté D0i.
Chacun de ces blocs passe par des fonctions de sélection (appelées parfois
boîtes de substitution ou fonctions de compression), notées généralement Si.
Voici la première fonction de substitution, représentée par une matrice de 4 par 16 :
Soit D01 égal à 101110. Les premiers et derniers bits donnent 10, c'est-à-dire 2 en binaire. Les bits 2,3,4 et 5 donnent 0111, soit 7 en binaire. Le résultat de la fonction de sélection est donc la valeur situé à la ligne n°2, dans la colonne n°7. Il s'agit de la valeur 11, soit en binaire 111. Chacun des 8 blocs de 6 bits est passé dans la fonction de sélection correspondante, ce qui donne en sortie 8 valeurs de 4 bits chacune. Voici les autres fonctions de sélection :
Chaque bloc de 6 bits est ainsi substitué en un bloc de 4 bits. Ces bits sont regroupés pour former un bloc de 32 bits.
Le bloc de 32 bits obtenu est enfin soumis à une permutation P dont voici la table :
L'ensemble de ces résultats en sortie de P est soumis à un OU Exclusif avec le G0 de départ (comme indiqué sur le premier schéma) pour donner D1, tandis que le D0 initial donne G1.
L'ensemble des étapes précédentes (rondes) est réitéré 16 fois.
A la fin des itérations, les deux blocs G16 et D16 sont "recollés, puis soumis à la permutation initiale inverse :
Le résultat en sortie est un texte codé de 64 bits !
Etant donné que l'algorithme du DES présenté ci-dessus est public, toute la sécurité repose sur la complexité des clés de chiffrement. L'algorithme ci-dessous montre comment obtenir à partir d'une clé de 64 bits (composé de 64 caractères alphanumériques quelconques) 8 clés diversifiées de 48 bits chacune servant dans l'algorithme du DES :
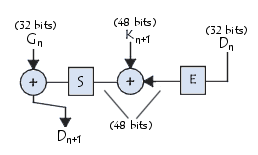
Dans un premier temps les bits de parité de la clé sont éliminés afin d'obtenir une clé d'une longueur utile de 56 bits. La première étape consiste en une permutation notée CP-1 dont la matrice est présentée ci-dessous :
Cette matrice peut en fait s'écrire sous la forme de deux matrice Gi et Di (pour gauche et droite) composées chacune de 28 bits :
On note G0 et D0 le réésultat;de cette première permutation. Ces deux blocs subissent ensuite une rotation à gauche, de telles façons que les bits en
seconde position prennent la première position, ceux en troisième position la seconde, ...
Les 2 blocs de 28 bits sont ensuite regroupés en un bloc de 56 bits. Celui-ci passe par une permutation, notée CP-2, fournissant en sortie un bloc de 48 bits, représentant la clé Ki.
Des itérations de l'algorithme permettent de donner les 16 clés K1 à K16 utilisées dans l'algortihme du DES.
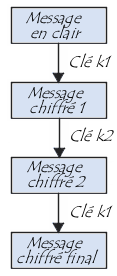
En 1990 Eli Biham et Adi Shamir ont mis au point la cryptanalyse différentielle qui recherche des paires de texte en clair et des paires de texte chiffrées. Cette méthode marche jusqu'à un nombre de rondes inférieur à 15, or un nombre de 16 rondes sont présentes dans l'algorithme présenté ci-dessus. D'autre part, même si une clé de 56 bits donne un nombre énorme de possibilités, de nombreux processeurs permettent de calculer plus de 106 clés par seconde, ainsi, utilisés parallèlement sur un très grand nombre de machines, il devient possible pour un grand organisme (un Etat par exemple) de trouver la bonne clé... Un solution à court terme consiste à chaîner trois chiffrement DES à l'aide de deux clés de 56 bits (ce qui équivait à une clé de 112 bits). Ce procédé est appelé Triple DES, noté TDES (parfois 3DES ou 3-DES).
Le TDES permet d'augmenter significativement la sécurité du DES, toutefois il a l'inconvénient majeur de demander également plus de ressources pour les chiffrement et le déchiffrement. En 1997 le NIST lança un nouvel appel à projet pour élaborer l'AES (Advanced Encryption Standard), un algorithme de chiffrement destiné à remplacer le DES. Le système de chiffrement DES fût réactualisé tous les 5 ans. En 2000 lors de la dernière révision, après un processus d'évaluation qui a duré 3 années, l’algorithme conçu conjointement par deux candidats belges, Messieurs Vincent Rijmen et Joan Daemen fût choisi comme nouveau standard par le NIST. Ce nouvel algorithme baptisé RIJNDAEL par ses inventeurs, remplacera dorénavant le DES.
L'algorithme du DES étant public (tout comme celui
du TDES ou de l'AES), vous pouvez accéder aux spécifications
sur le site du NIST :


|