|
|
Le codage binaire est très pratique pour une utilisation dans des appareils électroniques tels qu'un ordinateur, dans lesquels l'information peut être codée grâce à la présence ou non d'un signal électrique. Cependant le signal électrique peut subir des perturbations (distortion, présence de bruit), notamment lors du transport des données sur un long trajet. Ainsi, le contrôle de la validité des données est nécessaire pour certaines applications (professionelles, bancaires, industrielles, confidentielles, relatives à la sécurité, ...). C'est pourquoi il existe des mécanismes permettant de garantir un certain niveau d'intégrité des données, c'est-à-dire de fournir au destinataire une assurance que les données reçues sont bien similaires aux données émises. La protection contre les erreurs peut se faire de deux façons:
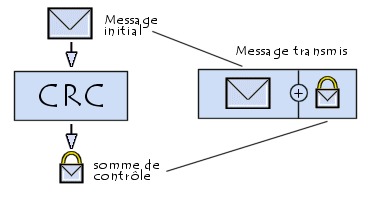
La plupart des systèmes de contrôle d'erreur au niveau logique sont basés sur un ajout d'information (on parle de "redondance") permettant de vérifier la validité des données. On appelle somme de contrôle cette information supplémentaire.
C'est ainsi que des systèmes de détection d'erreur plus perfectionnés ont été mis au point, ces codes sont appelées
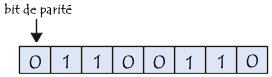
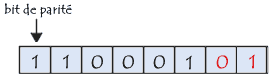
Le contrôle de parité (appelé parfois VRC, pour Vertical Redundancy Check ou Vertical Redundancy Checking) est un des systèmes de contrôle les plus simples. Il consiste à ajouter un bit supplémentaire (appelé bit de parité) à un certain nombre de bits de données appelé mot de code (généralement 7 bits, pour former un octet avec le bit de parité) dont la valeur (0 ou 1) est telle que le nombre total de bits à 1 soit pair. Pour être plus explicite il consiste à ajouter un 1 si le nombre de bits du mot de code est impair, 0 dans le cas contraire. Prenons l'exemple suivant:
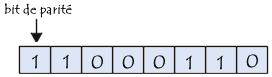
Dans cet exemple, le nombre de bit de données à 1 est pair, le bit de parité est donc positionné à 0. Dans l'exemple suivant, par contre, les bits de données étant en nombre impair, le bit de parité est à 1. :
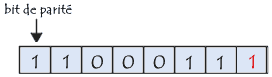
Imaginons désormais qu'après transmission le bit de poids faible (le bit situé à droite) de l'octet précédent soit victime d'une interférence:
Le bit de parité ne correspond alors plus à la parité de l'octet: une erreur est détectée. Toutefois, si deux bits (ou un nombre pair de bits) venaient à se modifier simultanément lors du transport de données, aucune erreur ne serait alors détectée...
Le système de contrôle de parité ne détectant que les erreurs en nombre impair, il ne permet donc de détecter que 50% des erreurs. Ce système de détection d'erreurs possède également l'inconvénient majeur de ne pas permettre de corriger les erreurs détectées (le seul moyen est d'exiger la retransmission de l'octet erroné, ...).
Le contrôle de parité croisé (aussi appelé contrôle de redondance longitudinale ou Longitudinal redundancy Check, noté LRC) consiste non pas à contrôler l'intégrité des données d'un caractère, mais à contrôler l'intégrité des bits de parité d'un bloc de caractères. Soit "HELLO" le message à transmettre, en utilisant le code ASCII standard. Voici les données telles qu'elles seront transmises avec les codes de contrôle de parité croisé :
Le contrôle de redondance cyclique (noté CRC, ou en anglais cyclic redundancy check) est un moyen de contrôle d'intégrité des données puissant et facile à mettre en oeuvre. Il représente la principale méthode de détection d'erreurs utilisée dans les télécommunications.
Le contrôle de redondance cyclique consiste à protéger des blocs de données, appelés trames (frames en anglais). A chaque trame est associé un bloc données, appelé code de contrôle (parfois CRC par abus de langage ou FCS pour Frame Check Sequence dans le cas d'un code de 32 bits). Le code CRC contient des éléments redondants vis-à-vis de la trame, permettant de détecter les erreurs, mais aussi de les réparer.
Le principe du CRC consiste à traiter les séquences binaires comme des polynômes binaires, c'est-à-dire des polynômes dont les coefficients correspondent à la séquence binaire. Ainsi la séquence binaire 0110101001 peut être représenté sous la forme polynômiale suivante : 0*X9 + 1*X8 + 1*X7 + 0*X6 + 1*X5 + 0*X4 + 1*X3 + 0*X2 + 0*X1 + 1*X0 soit X8 + X7 + X5 + X3 + X0 ou encore X8 + X7 + X5 + X3 + 1 De cette façon, le bit de poids faible de la séquence (le bit le plus à droite) représente le degré 0 du polynôme (X0 = 1), le 4ème bit en partant de la droite représente le degré 3 du polynôme (X3), ... Une séquence de n bits constitue donc un polynôme de degré maximal n-1. Toutes les expressions polynômiales sont manipulées par la suite avec une arithmétique modulo 2. Dans ce mécanisme de détection d'erreur, un polynôme prédéfini (appelé polynôme générateur et noté G(X)) est connu de l'émetteur et le récepteur. La détection d'erreur consiste pour l'émetteur à effectuer un algortihme sur les bits de la trame afin de générer un CRC, et de transmettre ces deux éléments au récepteur. Il suffit alors au récepteur d'effectuer le même calcul afin de vérifier que le CRC est valide.
Soit M le message correspondant aux bits de la trame à envoyer et M(X) le polynôme associé. Appelons M' le message transmis, c'est-à-dire le message initial auquel aura été concaténé le CRC de n bits. Le CRC est tel que M'(X)/G(X)=0. Le code CRC est ainsi égal au reste de la division polynomiale de M(X) (auquel on a préalablement concatèné n bits nuls correspondant à la longueur du CRC) par G(X). Le plus simple est encore de prendre un exemple : prenons le message M de 16 bits suivant : 1011 0001 0010 1010 (noté B1 en hexadécimal). Prenons G(X) = X3 + 1 (représenté en binaire par 1001). Etant donné que G(X) est de degré 3, il s'agit d'ajouter 4 bits nuls à M : 10110001001010100000 Le CRC est égal au reste de la division de M par G :
10110001001010100000
1001...,..,.,.,.....
----...,..,.,.,.....
0100..,..,.,.,.....
0000..,..,.,.,.....
----..,..,.,.,.....
1000.,..,.,.,.....
0000.,..,.,.,.....
----.,..,.,.,.....
1000.,..,.,.,.....
1001,..,.,.,.....
----,..,.,.,.....
1111..,.,.,.....
1001..,.,.,.....
----..,.,.,.....
1100.,.,.,.....
1001.,.,.,.....
----.,.,.,.....
1101,.,.,.....
1001,.,.,.....
----,.,.,.....
1000.,.,.....
0000.,.,.....
----.,.,.....
10001,.....
1001,.,.....
----,.,.....
10000.,.....
1001.,.....
----
1111,.....
1001,.....
----,.....
1100.....
1001.....
----.....
1100....
1001....
----....
1010...
1001...
----...
0110..
0000..
----..
1100.
1001.
----.
1010
1001
----
0011
Pour créer M' il suffit de concaténer le CRC ainsi obtenu aux bits de la trame à transmettre :
M' = 1011000100101010 + 0011 M' = 10110001001010100011Ainsi, si le destinataire du message effectue la division de M' par G, il obtiendra un reste nul si la transmission s'est effectuée sans erreur :
10110001001010100011
1001...,..,.,.,...,,
----...,..,.,.,...,,
0100..,..,.,.,...,,
0000..,..,.,.,...,,
----..,..,.,.,...,,
1000.,..,.,.,.....
1001.,..,.,.,.....
----.,..,.,.,.....
0010,..,.,.,.....
0000,..,.,.,.....
----,..,.,.,.....
0101..,.,.,.....
0000..,.,.,.....
----..,.,.,.....
1010.,.,.,.....
1001.,.,.,.....
----.,.,.,.....
0110,.,.,.....
0000,.,.,.....
----,.,.,.....
1101.,.,.....
1001.,.,.....
----.,.,.....
1010,.,.....
1001,.,.....
----,.,.....
0111.,.....
0000.,.....
----
1110,.....
1001,.....
----,.....
1111.....
1001.....
----.....
1100....
1001....
----....
1010...
1001...
----...
0110..
0000..
----,,
1101,
1001,
----,
1001
1001
----
0
Les polynômes générateurs les plus couramment employés sont :

|