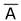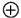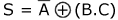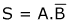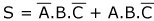|
|
Un processeur est composé de transistors permettant de réaliser des fonctions sur des signaux numériques. Ces transistors, assemblés entre eux forment des composants permettant de réaliser des fonctions très simples. A partir de ces composants il est possible de créer des circuits réalisant des opérations très complexes. L'algèbre de Boole (du nom du mathématicien anglais Georges Boole 1815 - 1864) est un moyen d'arriver à créer de tels circuits. L'algèbre de Boole est une algèbre se proposant de traduire des signaux en expressions mathématiques. Pour cela, on définit chaque signal élémentaire par des variables logiques et leur traitement par des fonctions logiques. Des méthodes (table de vérité) permettent de définir les opérations que l'on désire réaliser, et à transcrire le résultat en une expression algébrique. Grâce à des règles appelées lois de composition, ces expressions peuvent être simplifiées. Cela va permettre de représenter grâce à des symboles un circuit logique, c'est-à-dire un circuit qui schématise l'agencement des composants de base (au niveau logique) sans se préoccuper de la réalisation au moyen de transistors (niveau physique).
Un ordinateur ne manipule que des données binaires, on appelle donc variable logique une donnée binaire, c'est-à-dire une donnée ayant deux états possibles: 0 ou 1.
On appelle fonction logique une entité acceptant plusieurs valeurs logiques en entrée et dont la sortie (il peut y en avoir plusieurs) peut avoir deux états possibles: 0 ou 1. En réalité ces fonctions sont des composants électroniques admettant des signaux électriques en entrée, et restituent un signal en sortie. Les signaux électroniques peuvent prendre une valeur de l'ordre de 5 Volts (c'est l'ordre de grandeur général) que l'on représente par un 1, ou 0 V que l'on représente par un 0.
Les fonctions logiques de bases sont appelées portes logiques. Il s'agit de fonctions ayant une ou deux entrées et une sortie:
On définit généralement les fonctions NON OU (couramment appelée NOR) et NON ET (NAND) comme étant la composition respective d'un NON avec un OU et un ET.
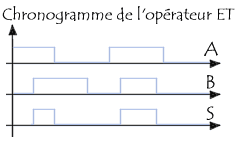
Un chronogramme est un diagramme montrant l'évolution des entrées et des
sorties en fonction du temps.
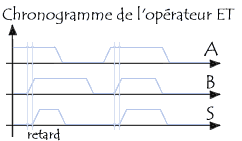
Ce chronogramme en un chronogramme idéal, en réalité les signaux électriques ne passent pas instantanément de 0 à 1, les pentes (ici verticales) sont obliques, et le traitement des entrées cause un retard sur les sorties:
Le but de l'algèbre de Boole est de décrire le traitement de signaux sous forme d'expression algébrique. Comme nous l'avons vu, les signaux sont représentés par des noms de variables. Les fonctions logiques sont représentées par des opérateurs:
Une expression algébrique sera donc une expression du type:
Une table de vérité est un tableau permettant de décrire toutes les possibilités de sorties en fonction des entrées. On place donc les variables d'entrées dans les colonnes de gauche en les faisant varier de telle façon à couvrir l'ensemble des possibilités. La colonne (ou les colonnes si la fonction a plusieurs sorties) de droite décrit la sortie. Voici par exemple les tables de vérités des portes logiques:
Il est possible à partir de la table de vérité d'une fonction d'écrire
l'expression algébrique de celle-ci.
La sortie vaut 1 lorsque A vaut 1 et B vaut 0, l'expression algébrique de cette fonction est donc:
Prenons maintenant la table de vérité suivante:
La sortie vaut 1 lorsque


| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||