
|
|
A partir des opérations de base de nombreuses opérations très utiles peuvent être définies. En voici quelques unes:
L'intersection entre deux tables est la table contenant l'ensemble des tuples (cellules) appartenant aux deux tables. Les deux tables opérandes doivent être de même schéma, c'est-à-dire que les attributs de la table (colonnes) doivent être les mêmes. On note l'intersection entre deux tables R1 et R2: inter(R1,R2)ou encore R1Cet opérateur peut être décrit à l'aide d'opérateurs de base: R1
Le quotient de deux tables est la table contenant l'ensemble des tuples (cellules) qui concaténés à chaque tuple de l'une des tables fournissent des tuples appartenant à l'autre On note le quotient de deux tables R1 et R2: div(R1,R2)ou encore R1/R2
On appelle θ-jointure selon une qualification Q l'ensemble des tuples provenant du produit cartésien de deux relations et satisfaisant la qualification, c'est-à-dire la condition exprimée à l'aide des comparateurs:
joinQ(R1,R2)ou encore (R1 On définit des types de jointure particulière selon la qualification Q:


|



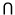 R2
R2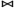 Q)R2
Q)R2